What is the probability that in a room of 23 people, at least two have the same birthday? (Ignore leap years and assume each day is equally likely.)
Solution
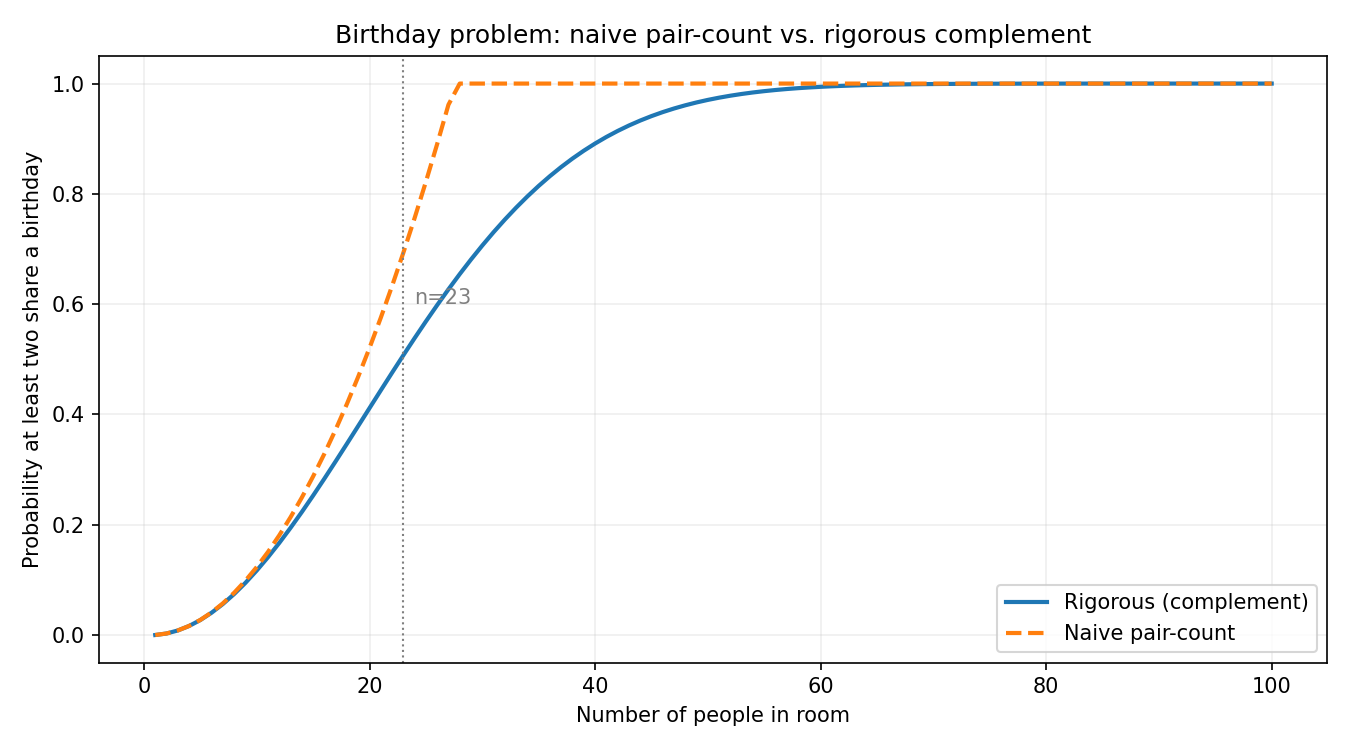
Quick (pair-count intuition)
Any pair among the 23 people could be the matching pair. The number of pairs is ${23 \choose 2}=253$. A very rough heuristic treats each pair as having probability $\tfrac{1}{365}$ of matching, giving the naive estimate $\dfrac{253}{365}\approx 0.693$. This is an overestimate because pairs' matching events are not independent.
Rigorous (complement method)
Compute the probability that all 23 birthdays are distinct, then subtract from 1. The probability all are distinct is
$$P(\text{all distinct})=\frac{365}{365}\cdot\frac{364}{365}\cdot\frac{363}{365}\cdots\frac{365-22}{365}=\prod_{k=0}^{22}\frac{365-k}{365}.$$
Therefore the desired probability is
$$P(\text{at least one match})=1-\prod_{k=0}^{22}\frac{365-k}{365}\approx 0.5073.$$
So with 23 people the probability that two share a birthday is about 50.7%.